NOMBOR BULAT
Nombor bulat terdiri daripada angka 0, 1, 2, 3, 4, 5, 6, 7, 8 dan 9 yang bolehditulis dalam perkataan atau angka.
Nombor 1, 2, 3, 4, ... dipanggil nombor tabii / asli (natural numbers). Set tiga titik dibelakang nombor-nombor tersebut menunjukkan bahawa corak terus-menerusnya yang juga dipanggil elipsis (ellipsis).
Setiap1,2,3,4.... bulat mewakili nilai tertentu mengikut kedudukan nilaiangka dalam nombor tersebut. Sebagai contoh, nilai bagi setiap angka dalamnombor 4,128,925 adalah seperti berikut;
Juta - angka 4
Ratus ribu - angka 1
Puluh ribu - angka 2
Ribu - angka 8
Ratus - angka 9
Puluh -angka 2
Unit - angka 5
Nilai bagi setiap angka dalam nombor boleh ditunjukkan dengan menggunakanjadual. Kedudukan angka dalam sesuatu nombor menunjukkan nilainya.
Nombor
Nilai angka 5
Nilai angka 3
5 643
5 000
3
2 358
50
300
.
Menghitung nombor bulat
Hitung dalam gandaan sepuluh dari 20 hingga 50
(Jwb: 20, 30, 40, 50)
Hitung dalam gandaan dua dari 4 hingga 20
(Jwb: 4, 6, 8, 10, 12, 14, 16, 18, 20)
Hitung dalam pengurangan lima dari 30 hingga 10
(Jwb: 30, 25, 20, 15, 10)
Hitung dalam pengurangan seratus dari 1100 hingga 500
(Jwb: 1100, 1000, 900, 800, 700, 600, 500)
Menulis nombor bulat dalam perkataan
1 020 (Jwb: Seribu dua puluh)
19 503 (Jwb: Sembilan belas ribu lima ratus tiga)
634 202 (Jwb: Enam ratus tiga puluh empat ribu dua ratus dua)
1 007 032 (Jwb: Satu juta tujuh ribu tiga puluh dua)
Menulis nombor bulat dalam bentuk angka
Lima ratus tiga puluh empat (Jwb: 534)
Dua belas ribu tujuh puluh (Jwb: 12 070)
Lima ratus dua puluh empat ribu, dua ratus empat puluh dua (Jwb: 524 242)
Dua puluh satu juta, tujuh ribu empat puluh lapan (Jwb: 21 007 048)
Mengenal pasti nilai tempat
24 763
2 - puluh ribu
4 - ribu
7 - ratus
6 - puluh
3 - unit
374 125
3 - ratus ribu
7 - puluh ribu
4 - ribu
1 - ratus
2 - puluh
5 - unit
Mengenal pasti nilai angka dalam nombor bulat
Kenal pasti nilai angka 6 dalam nombor 36 052
Jwb: Nilai tempat angka 6 adalah ribu. Oleh itu nilai angka 6 adalah 6000.
Kenal pasti nilai angka 7 dalam nombor 472 351
Jwb: Nilai tempat angka 7 adalah puluh ribu. Oleh itu nilai angka 7 adalah 70 000.
Nombor bulat boleh di'bundarkan' (rounded off) kepada nilai tempat tertentu mengikut ketepatan yang diperlukan.
Kaedah untuk pembundaran (rounding off) nombor bulat kepada nilai tempat yang diberi adalah seperti berikut;
Cari angka di sebelah kanan nilai tempat yang diberi.
Jika angka ini adalah kurang dari 5, biarkan angka pada nilai tempat tersebut tidak berubah.
Jika angka ini adalah 5 atau lebih, maka tambahkan 1 pada angka dalam nilai tempat yang diberi dan gantikan setiap angka di sebelah kanan dengan 0.
Pembundaran nombor bulat
Bundarkan 37 268 yang nilai yang terhampir
Ribu
Nilai tempat yang diberi, ribu = 7.
Angka disebelah kanan nilai tempat yang diberi adalah 2 (2<5 ).
Biarkan angka 7 tidak berubah dan gantikan kesemua angka di sebelah kanan angka 7 dengan 0.Oleh itu pembundaran 37 268 kepada nilai ribu yang terhampir adalah 37 000.
Puluh ribu
Nilai tempat yang diberi, puluh ribu = 3.
Angka disebelah kanan nilai tempat yang diberi adalah 7 (7>5).
Tambahkan 1 pada angka 3 dan gantikan kesemua angka di sebelah kanan angka 3 dengan 0.Oleh itu pembundaran 37 268 kepada nilai puluh ribu yang terhampir adalah 40 000.
Bab 2 Pola dan Turutan Nombor
Corak/Pola Nombor dan Urutannya
Nombor-nombor yang disusun dalam corak tertentu dikenali sebagai urutan (sequence).
Corak urutan nombor (number sequence) boleh ditentukan dengan menambah, menolak, mendarab atau membahagikan ‘nombor dalam urutan yang sebelumnya’, dengan bilangan/nombor-nombor tertentu.
Urutan Fibonacci (Fibonacci Sequence)
Ahli matematik telah mengkaji corak selama berabad-abad. Corak nombor 1, 1, 2, 3, 5, 8, …dipanggil urutan Fibonacci.
Urutan ini bermula dengan 1, 1 dan setiap selepas sebutan (term) yang kedua, diperolehi dengan menambah dua sebutan (term) sebelumnya yang terdapat dalam urutan.
Menggambarkan corak/pola urutan nomborGambarkan corak setiap urutan nombor berikut:
- 5, 12, 19, 26, …
Jwb:
Corak urutan nombor 5, 12, 19, 26, … diperolehi dengan menambah (adding) 7 pada nombor sebelumnya (nombor dalam urutan). - 1, 4, 16, 64, …
Jwb:
Corak urutan nombor 1, 4, 16, 64, … diperolehi dengan mendarabkan (multiplying) nombor dalam urutan sebelumnya dengan 4. - 40, 35, 30, 25, …
Jwb: - 144, 72, 36, 18, …
Jwb:
Corak urutan nombor 144, 72, 36, 18, … diperolehi dengan membahagikan (dividing) nombor dalam urutan sebelumnya dengan
Bab 3 Pecahan
Pecahan
Apabila satu unit dari keseluruhan kuantiti dibahagikan kepada bahagian yang sama, mana-mana bahagian dalam kuantiti tersebut dipanggil sebagai pecahan unit (fractions of the unit).
Jadual dibawah menunjukkan bagaimana pecahan dibaca.
Pecahan adalah nombor yang mewakili satu atau lebih bahagian yang sama dibahagikan daripada keseluruhannya. Contohnya, Dalam rajah dibawah, setiap bahagian adalah 1 daripada 6 bahagian yang sama.
Pecahan juga boleh digunakan untuk menamakan sebahagian daripada koleksi atau satu set objek atau kumpulan. Contohnya,
Setiap pensil di atas adalah 1 daripada sekumpulan 4 pensel.
Pecahan boleh diwakili oleh gambar rajah. Contohnya,
Bahagian-bahagian yang berlorek dalam gambar rajah adalah mewakili 8 bahagian daripada 9 bahagian yang sama. Dengan kata lain, 8/9 daripada gambar rajah.
Menulis pecahan.
Pecahan ditulis dalam bentuk , dimana a adalah pengangka (numerator) dan b adalah penyebut (denominator). Contohnya,
, dimana a adalah pengangka (numerator) dan b adalah penyebut (denominator). Contohnya,
 , dimana a adalah pengangka (numerator) dan b adalah penyebut (denominator). Contohnya,
, dimana a adalah pengangka (numerator) dan b adalah penyebut (denominator). Contohnya,
Bilangan 1 adalah mewakili semua bahagian keseluruhannya.
Contoh 1:
Apakah pecahan yang diwakili oleh bahagian-bahagian yang berlorek dalam setiap gambar rajah di bawah?
- Jwb: 5/8
- Jwb: 1/4
- Jwb: 3/6 = 1/2
Bab 4 Nombor Perpuluhan
Nombor Perpuluhan dan Pecahan
Mewakilkan pecahan 1/10 dan 1/100 sebagai nombor perpuluhan dan sebaliknya.
Nombor perpuluhan (decimals) adalah pecahan (fractions) yang mana penyebutnya (denominator) adalah gandaan 10, iaitu, 10, 100, 1 000, … dan seterusnya.
Dalam rajah di bawah, kawasan berlorek mewakili 8 daripada 10 bahagian, iaitu 8/10 bahagian.
1 daripada 10 bahagian = 1/10 = 0.1
Disebabkan 1/10 = 0.1
Oleh sebab itu, 8/10 = 0.1 x 8 = 0.8
Oleh itu, nombor perpuluhan dan pecahan, adalah boleh saling ditukar(interchangeable).
Mewakilkan pecahan dengan penyebut 1, 100 dan 1 000 sebagai nombor perpuluhan.
Mana-mana pecahan dengan penyebut (denominator) 10, 100 dan 1 000 boleh diungkapkan dalam bentuk nombor perpuluhan.
Disebabkan 1/10 = 0.1,
dan 1/100 = 0.01,
dan 1/1000 = 0.001,
Oleh sebab itu 81/100 = 0.81
Bagaimana nombor perpuluhan ditulis dan dibaca?
- 4/10 = 0.4 [dibaca sebagai: kosong perpuluhan empat (zero point four)]
- 3/100 = 0.03 [dibaca sebagai: kosong perpuluhan kosong tiga (zero poit zero three)]
- 1987/1000 = 1.987 [dibaca sebagai: satu perpuluhan sembilan lapan tujuh (one point nine eight seven)]
Menukarkan pecahan kepada nombor perpuluhan dan sebaliknya.
Untuk menukar pecahan kepada nombor perpuluhan:
- Bahagikan pengangka (numerator) oleh penyebutnya (denominator).
Contoh 1:
Tukarkan pecahan berikut kepada nombor perpuluhan.
Tukarkan pecahan berikut kepada nombor perpuluhan.
Untuk menukar nombor perpuluhan kepada pecahan:
- Kira bilangan digit di sebelah kanan titik perpuluhan.
- Kemudian, tukarkan nombor perpuluhan kepada pecahan yang setara, dengan penyebutnya adalah gandaan 10.
- Permudahkan jawapan kepada sebutan (term) yang paling rendah (serendah mungkin).
Contoh 2:
Tukarkan nombor perpuluhan berikut kepada pecahan.
Tukarkan nombor perpuluhan berikut kepada pecahan.
- 0.07
Jwb:
0.07 = 7/100
0.07 (mempunyai dua digit disebelah kanan titik perpuluhan)
7/100 (penyebutnya mempunyai dua sifar/zero) - 0.095
Jwb:
0.095 = 95/1000
0.095 (mempunyai tiga digit disebelah kanan titik perpuluhan)
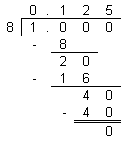
95/1000 (penyebutnya mempunyai tiga sifar/zero) - 1.568
Jwb:
1.568 = 1 + 0.568 = 1 + 568/1000
Bab 5 Peratus
Peratusan
Pecahan dengan 100 sebagai penyebut (denominator) dipanggil sebagaiperatusan (percentage). Dalam kes ini, pengangka (numerator) mewakili nombor/bilangan bahagian-bahagian dalam setiap 100.
Simbol % digunakan bagi mewakili peratusan.
Contoh 1:
80/100 dinyatakan sebagai 80%, dimana;
80/100 dinyatakan sebagai 80%, dimana;
- 80/100 adalah pecahan dengan 100 sebagai penyebut,
- 80% dibaca sebagai ‘lapan puluh peratus’ (eighty per cent).
14% dinyatakan sebagai 14/100.
Contoh 2:
Ungkapkan 53% sebagai suatu pecahan (fraction).
Jwb:
53% = 53/100
Ungkapkan 53% sebagai suatu pecahan (fraction).
Jwb:
53% = 53/100
Menukarkan pecahan dan perpuluhan kepada peratusan, dan sebaliknya.
Untuk menukar pecahan atau nombor perpuluhan kepada peratusan:
- Kaedah 1: Tukarkan penyebut (pecahan) kepada 100.
- Kaedah 2: Darabkan pecahan atau nombor perpuluhan dengan 100%.
Contoh 3:
Ungkapkan setiap nilai berikut sebagai peratusan.
Ungkapkan setiap nilai berikut sebagai peratusan.
- 2/5
Jwb:
2/5 = (2 x 20) / (5 x 20) = 40/100 = 40%
atau 2/51 x 10020% = 40% - 1/2
Jwb:
1/2 = (1 x 50) / (2 x 50) = 50/100 = 50%
atau 1/21 x 10050% = 50% - 0.3
Jwb:
0.3 = 3/10 = (3 x 10) / (10 x 10) = 30/100 = 30%
atau 0.3 x 100% = 30% - 0.42
Jwb:
0.42 = 42/100 = 42%
atau 0.42 x 100% = 42%
Untuk menukar peratusan ke dalam pecahan atau perpuluhan:
Bahagikan peratusan tersebut dengan 100%.
Bahagikan peratusan tersebut dengan 100%.
Contoh 4:
Tukarkan setiap yang berikut kepada:
i) Pecahan
ii) Nombor perpuluhan (decimal number)
Tukarkan setiap yang berikut kepada:
i) Pecahan
ii) Nombor perpuluhan (decimal number)
- 85%
Jwb:
i) 85% = 85/100 = 17/20 (Jawab dalam pecahan yang terendah)
ii) 85% = 85/100 = 0.85 (Jawab dalam bentuk perpuluhan) - 48%
Jwb:
i) 48% = 48/100 = 12/25 (Jawab dalam pecahan yang terendah)
ii) 48% = 48/100 = 0.48 (Jawab dalam bentuk perpuluhan)
Bab 6 :INTEGER
Integer
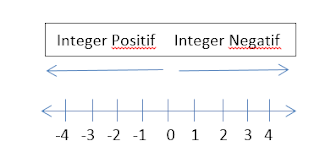
- Integer ialah nombor bulat yang mempunyai tanda positif atau negatif dan sifar yang berada diantara kawasan ini.
- Pada integer nombor sebelah kiri sifar ialah integer negatif manakala disebelah kanan pula ialah integer positif
- Penambahan dan penolakan integer
Bab 7 Ungkapan Algebra (l)
1. An unknown is a quantity whose value is not known.
2. An unknown can be represented by a symbol or a letter.
3. An algebraic term with one unknown is the product of an unknown and a number
. The number is known as the coefficient.
For example:
5p
Coefficient Unknown
4. Like terms are that have the same unknown.
For example:
2k , 3k
5. Unlike terms are term that have different unknowns.
For example:
-3m , 2n , 6p
6. An algebraic expression consists of two or more terms that combined by addition
or subtraction or both of the operations.
For example:
3x + 4y - 6 is an expression with three terms.
7. The like terms in an algebraic expression can be simplified by adding or
subtracting the coefficients of the unknowns in the algebraic terms.
For example:
x + 4y + 2x – 3y = x + 2x +4y – 3y
= 3x + y
ENRICHMENT PRACTICE
M students from N society have collected p kg of old
newspapers and q kg of tins in a recycling campaign.
State the letters that represent the unknowns and objects.
2. What is the coefficient of -12a?
3. Diagram 1 shows a list of algebraic terms.
-13h , 6k , -1⁄4 h , 1.2h , k/5
Diagram 1
State all the like terms of 3h
4. Determine the number of terms in the expression 5x + y + 3x – 4y – 2
5. Simplify x + y + 4y + x + 2x
6. The weight of an empty basket is 5y kg. The total weight of the basket filled with
durian is (7y – 3) kg. Find the weight , in kg , of the durian.
7. Simplify 1⁄3p + 3q + 2p – 2q
8. Simplify 6x – y – (-x) + y
9. Simplify 5m – n – 4m – 2n + 7
10. Hassan is (5x + 23) years old. His son is 7x years old. Find the difference between
their age in terms of x.
CHAPTER 8
BASIC MEASUREMENTS
-
LENGTH
A) Determining the Metric Units of Length
1. Lenght is the distance between two points. 2. The relationships between the metric units of legth are shown below : Worked Example 1 State the units of length suitable for measuring (a) the thickness of a coin, (b) the length of Sungai Pahang. Solution (a) mm (b) km B) Conversion between Metric Units of length A unit of length can be converted to another unit. (a) 1 cm = 10 mm (b) 1 m = 100 cm (c) 1 m = 100 x 10 mm = 1 000 m (d) 1 km = 1 000 m (e) 1 km = 1 000 x 100 cm = 100 000 cm (f) 1 km = 100 000 x 10 mm = 1 000 000 mm Worked Example 2 Convert (a) 31 m to cm, 4 (b) 26 cm 2 mm to mm Solution Worked Example 3 Convert (a) 62.3 cm to m, (b) 1 km 25 m to km. Solution Worked Example 4 Convert (a) 85 mm to cm and mm, (b) 6 054 Solution Worked Example 5 Convert (a) 73 m to m and cm, 4 (b) 0. 52 km to cm. Solution C) Measuring the Lengths of Objects Worked Example 6 Measure the length of the straight line PR with a ruler. Solution PR = 2.8 cm or 2 cm 8 mm Worked Example 7 Mesure the curve MN. Solution Use a piece of thread and place it on the curve from M to N. Mark the point N on it. Stretch the thread on a ruler to mesure the length of the curve MN. MN = 4.6 cm or 4 cm 6 mm D) Drawing Straight Lines Use A straight line can be drawn by using a ruler and a pencil if the length is given. Worked Example 8 Draw the straight line PR with the length of (a) 41 cm (b) 6 cm 4 mm. 2 Solution E) Estimating the Lengths of Objects When estimating the length of an object, an appropriate unit of length must be used. For example :- The appropriate unit of measurement for estimating the thickness of a coin is mm. Other units of length such as m and km are not suitable in this case. m and km are used for larger measurement. Worked Example 9 Estimate the length of the fluorescent tube in metres. Solution The estimated length of the fluorescent tube is 1. 5 m. The actual length is 1. 22 m. F) Addition, Subtraction, Multiplication and Division involving Length Estimate Before performing addition, subtraction, multiplication or division involving lengths of different units, we have to change all the measurements to the same unit first. Worked Example 10 Solve (a) 15 m 42 cm + 6 m 25 cm (b) 24. 9 cm + 4 mm. Solution Therefore, 15 m 42 cm + 6 m 25 cm = 21 m 67 cm Worked Example 11 Solve (a) 6 cm - 2. 015 cm, (b) 51 mm - 23 mm, 2 10 (c) 33. 52 m - 16 cm. Solution (a) 6. 000 cm - 2. 015 cm 3. 985 cm Therefore, 6 cm - 2. 015 cm = 3. 985 cm Worked Example 12 Solve (a) 64 mm x 8 8 (b) 4 km 20 m 12 cm x 5 Solution (a) 64 mm x 8 8 = 52 mm x 8 8 = 52 mm Therefore, 4 km 20 m 12 cm x 5 = 20 km 100 m 60 cm Worked Example 13 Solve (a) 18. 2 cm ÷ 5 (b) 15 km 280 ÷ 4. Solution G) Problem Solving involing Length Worked Example 14 A piece of black thread is 2 m 64 cm long and a piece of red thread is 2. 4 m long. Find their total length. Solution 1. Understand the problem Length of the black thread = 2 m 64 cm Length of red thread is 4. 6 m Find : Total length of the two pieces of threads 2. Devise a plan Change 2 m 64 cm to m and then nuse addition. 3. Carry out the plan 2 m 64 cm = 2 m + ( 64 ÷ 100) m = 2 m + 0. 64 m = 2. 64 m 2. 64 m + 2. 4 m = 5. 04m 2. 64 m + 2. 40 m 5. 04 m Therefore, the total length is 5. 04 m. 4. Check 5. 04 m - 2. 4 m 2. 64 m MASS A) Determining the Metric Units of Mass 1. Mass is the amount of matter in an object. 2. Mass is usually measured in grams (g), kilograms (kg) and tonnes in metric units. 3. A suitable unit of measured should be used for determining the mass of an object. Worked Example 15 State suitable unit for each of the following. (a) The mass of a chicken (b) The mass of an egg Solution (a) kg (b) g B) Conversion between Metric Units of Mass The relationships between the units of mass in the metric system are as follows. Worked Example 16 Convert (a) 2. 45 kg to g, (b) 3 106 kg to tonnes, (c) 15 030 g to kg and g, (d) 67. 05 Solution C) Measuring the Mass of Objects 1. A weighing machine is used to measure the mass of an object. 2. Before weighing the object, the pointer (needle) must be set at zero. Worked Example 17 State the mass of each object on the weighing machine below. (a) (b) Solution (a) 300 g (b) 1. 8 kg D) Estimating the Mass of Object When estimating the mass of an object, an appopriate unit of mass must be used. For Example :- The unit suitable for measuring the mass of a 20 sen coin is g. kg is not suitable in this case as kg is used for larger measurements. Worked Example 18 Estimate the mass of (a) a bottle of 300 ml of mineral water, (b) a ream of A4 papers. Solution (a) Using a packet of 300 g of sugar as a guide, the estimated mass of the bottle of mineral water is about 300 g. The actual mass of the bottle of mineral water is 310 g. (b) Using a packet of flour weighing 1 kg as a guide, the mass of a ream of A4 paper is estimated to be about 2 kg. The actual mass of a ream of A4 paper is 2. 38 kg. E) Addition, Subtraction, Multiplication and Division involving Mass Before performing addition, subtraction,multip- lication and division involving mass, change all the measurements to the same unit. Worked Example 19 Solve (a) 8 tonnes 350 kg + 6 tonnes 740 kg, (b) 13 kg 70 g - 4 kg 520 g (c) 720 g - 3 kg 5 Solution Worked Example 20 Solve (a) 5 tonnes 410 kg x 6 (b) 22 kg ÷ 4 5 (c) 20 kg 25 g ÷ 8 Solution F) Problem Solving involving Mass An empty vessel weights 530 g. When filled with sugar, it weights 2. 58 kg. Find, in kg, the mass of the sugar. Solution 1. Understand the problem Given information : Mass of the empty vessel = 530 g Mass of the empty vessel + sugar = 2. 58 kg Find : Mass of sugar 2. Devise a plan Change the mass of the empty vessel to kg and then use subtraction. 3. Carry out the plan 530 g = ( 530 ÷ 1 000 ) kg 0. 53 kg 2. 5 8 kg - 0. 5 3 kg Mass of sugar 2. 0 5 kg = 2. 58 kg - 0. 53 kg = 2. 05 kg Therefore, the mass of the sugar is 2. 05 kg. 4. Check 2. 05 kg + 0. 53 kg 2. 58 kg TIME A) Determining the Appropriate Units of Time 1. Time is the period between two occurrences or events. 2. The units of time are seconds, minutes, hours, days, weeks, months, years, decades, centuries and millenniums. Worked Example 22 State a suitable unit of time for each of the following. (a) The age of a person (b) The time taken to travel from Shah Alam to Kuala Pilah by car Solution (a) Years and months (b) Hours and minutes B) Conversion between Units of Time State a The relationships between the units of time are as follows : Worked Example 23 Convert (a) 51 days to hours, 4 (b) 6 minute 18 seconds to seconds. Solution (a) 51 days = 21 x 24 hours 4 4 = 126 hours (b) 6 minute 12 seconds = ( 6 x 60 ) seconds + 18 seconds = ( 360 + 18 ) seconds = 378 seconds Worked Example 24 Convert (a) 36 months to years, (b) 309 minutes to hours and minutes. Solution (a) 32 months = ( 36 ÷ 12 ) years = 3 years C) Measuring the Time taken for an Activity A stop watch or a digital clock are always used to measure he time taken for an activity. The units used are usually in seconds, minutes and hours. D) Estimating the Time of an Activity Estimate the time taken to sing the national anthem, "Negaraku". Solution 30 seconds E) Addition, Subtraction, Multiplication and Division involving Time Worked Example 26 Solve (a) 5 minutes 42 seconds + 31 minutes. 2 Solution (a) 5 minutes 42 seconds + 31 minutes 2 = 5 minutes 42 seconds + 3 mminutes 30 seconds = 9 minutes 12 seconds Worked Example 27 Solve (a) 14 weeks 2 days - 6 weeks 5 days (b) 22. 3 minutes - 24 seconds Solution (b) 22. 3 minutes - 24 seconds = ( 22 + 0. 3) minutes - 24 seconds = 22 minutes + ( 0. 3 * 60 ) seconds - 24 seconds = 22 minutes 18 seconds - 24 seconds = 21 minutes 54 seconds Worked Example 28 Solve (a) 8 days 15 hours x 4 Solution Worked Example 29 Solve (a) 7 hours ÷ 12 Solution (a) 7 hours ÷ 12 = ( 7 x 60 ) minutes ÷ 12 = 420 minutes ÷ 12 = 35 minutes F) Problem Solving involving Time Worked Example 30 A bus took 6 hours 35 minutes to travel from Seremban to Ipoh. It took another 2 hours 15 minutes to travel from Ipoh to Butterworth. Calculate the total time taken to travel from Seremban to Butterworth. Solution 1. Understand the problem Given information : Seremban to Ipoh = 6 hours 35 minutes Ipoh to Butterworth = 2 hours 15 minutes Find : Total time from Shah Alam to Butterworth 2. Devise a plan Use addition. 3. Carry out the plan 4. Check 8.4 TWELVE-HOUR AND TWENTY- FOUR-HOUR SYSTEM A) Time in the 12-hour System 1. Time can be expressed in the 12-hour system or 24-hour system. 2. In the 12-hour system, we have to state clearly whether the time is in the morning, noon, after- noon, evening, night or midnight. 3. In the 12-hour system, a.m. is used for the time between midnight and noon whereas p.m. is used for the time between noon and midnight. Solution For example :- Worked Example 31 Write the time for each of the following in the 12- hour system. (a) (b) Solution (a) 8. 20 a.m. (b) 3. 35 p.m. B) Time in the 24-hour System 1. In the 24-hour system, four digits are used to indicate time. The first two digits denote hour and the last two digits dennite minutes. For example :- 2. A day ends at 2400 hours. The next day begins at 0000 which is 12. 00 midnight. Worked Example 32 Write the time for each of the following in the 24- hour system. (a) (b) Solution (a) 0805 hours (b) 1120 hours C) Changing Time in the 12-hour System to the 24-hour System and vice versa The relationship between the times in two systems is shown below. Worked Example 33 Change each of the following to the 24-hour system. (a) 8. 15 a.m. (d) 10 .45 p.m. (b) 11. 00 a.m. (e) 12. 20 a.m. (c) 4. 35 p.m. Solution Worked Example 34 Change each of the following to the 12-hour system. (a) 0925 hours (c) 1705 hours (b) 1235 hours (d) 0045 hours Solution D) Determining the Interval between Two given Times Interval is the length of time between two given times. Worked Example 35 Find the interval between 09.15 a.m. and 3. 45 p.m. on the same day. Solution Interval = 2 hours 45 minutes + 3 hours 45 minutes = 6 hours 30minutes Worked Example 36 Find the interval between 11. 30 p.m. on Tuesday and 4. 15 a.m. on Wednesday. Solution Interval = 30 minutes + 4 hours 15 minutes = 4 hours 45 minutes E) Determining the Time in the 12-hour System or 24-hour System Worked Example 37 Find the time which is 5 hours 25 minutes after 2. 15 p.m., in the 12-hour system. Solution The time is 7. 40 p.m.. Worked Example 38 Find the time which is 5 hours 55 minutes before 2. 10 p.m., in the 12-hour System. Solution 2. 10 p.m. = 1410 hours The time is 8. 15 a.m.. Worked Example 39 Find the time which is 4 hours 50 minutes after 2120 hours, in the 12-hour system. Solution The time is 0210 hours, the next day. F) Problem Solving involving Time A show starts at 8. 45 a.m. and ends at 3. 20 p.m. How long is the show? Solution 1. Understand the problem Given information : The show starts at 8. 45 a.m.. The show ends st 3. 20 p.m.. Find : Duration of the show 2. Devise a plan Change the times to the 24-hour system and then use subtraction. 3. Carry out the plan 8. 45 a.m. = 0845 hours 3. 20 p.m. = 1520 hours Therefore, the show lasts 6 hours 35 minutes. 4. Check |
copyright © 2005 Kenshido International Sdn Bhd
|
CHAPTER 9
LINES AND ANGLES
ANGLES
A) Identifying an Angle
angle is formed by two straigth lines that meet
at a point called the vertex.
For example : -
In the figure above,
(a) AOB is an angle.
(b) OA and OB are called the arms of the angle.
(c) O is the vertex, that is the point where the two
arms meet.
Worked Example 1
Mark the angle in each case.
(a) (b)
Solution
(a) (b)
B) Naming an angle
An angle can be named by using one letter
or three letters.
For example :-
Worked Example 2
C) Measuring Angles
1. Angles are measured in units called degrees
( 0 ).
2. To measure an angle, we can use an instru-
ment called the protractor as shown below.
3. Note that if we read from left to right ( clockwise
direction ), we use the inner scale.
4. To measure an angle less than 1800, <KLM, follow
the steps below.
Method 1 :
Step 1
Place the protactor that its centre is on the vertex
L. Adjust the protractor until its base line corresponds
with the arm LM.
Step 2
Read the value of <KLM using the inner scale.
Therefore, <KLM = 300.
Method 2 :
Step 1
Place the protractor so that its centre is on the
vertex L. Adjust the protractor until its base line
corresronds with the arm LK.
Step 2
Read the value of <KLM using the outer scale.
Therefore, .KLM = 300
5. To measure an angle which is more than 1800,
follow the steps below :
To measure <STU
Step 1
Produce the arm ST to V and measure <STV.
<STV = 1800
Step 2
Place and adjust the protractor as shown to
measure <VTU.
Step 3
<STU = <STV + <VTU
= 1800 + 200
= 2000
D) Drawing Angles Using a Protractor
1. We can also use a protractor to draw an angle.
2. To draw <RST =600, follow the steps below.
Step 1
Draw an arm ST with S as the vertex.
Step 2
Place the protractor so that its centre is on the
vertex S and its base line is on ST.
Step 3
Find 600 at the inner scale and mark it with a point.
Call this point R.
Step 4
Remove the protractor and draw a line to join R
with S.
Step 5
Mark and label <RST as 600.
3. To draw <KLM = 2400 ( more than 1800 ), follow the
steps below.
Step 1
Draw an arm KL with L as the vertex.
Step 2
Place the protractor so that its centre is on the
vertex L and its base line is on KL. Mark the
point M at 600 on the outer scale.
Step 3
Remove the protractor and join LM with a straight
line.
Step 4
Label <KLM as 2400.
E) Identifying the Different Types of Angles
The table below shows the different types of angles.
Worked Example 3
Which of the following angles is acute, obtuse,
reflex or right-angled?
(a) 1650
(b) 900
(c) 2340
(d) 830
Solution
(a) 1650 is an obtuse angle.
(b) 900 is right angle.
(c) 2340 is a reflex angle.
(d) 830 is an acute angle.
G) Determining the Sum of Angles on a
Straight Line
1. Use a protractor to measure the angles on the
straight line.
Worked Example 4
Using a protractor, measure the angles on the
straingh line KLM. Then, find the sum of the
angles in each case.
(a) (b)
Solution
(a) x = 1200 , y = 600
x + y = 1200 + 600
= 1800
(b) p = 400 , q = 900 , r = 500
p + q + r = 400 + 900 + 500
= 180
2. In general, the sum of the angles on a straight
line is 1800.
For example :-
AOB is a straight line.
x + y + z = 1800
H) Determining the Sum of Angles in
One Whole Turn
1. A protractor is used to measure the angles
at a point.
Worked Example 5
Use a protractor to measure the angles in the
figures. Then, find the sum of the angles in each
case.
(a) (b)
Solution
(a) x = 1100 , y = 2500
x + y = 1100 + 2500
= 3600
(b) p = 1300 , q = 600 , r = 700 , s = 1000
p + q + r + s = 1300 + 600 + 700 + 1000
= 3600
2. In general, the sum of the angles that formed
one whole turn is 3600.
For example :-
a + b + c + d + e = 360
I) Calculating Angles involving One
Whole Turn
Worked Example 6
Without measuring, calculate the angles marked.
(a)
(b)
Solution
PARALLEL LINES AND
PERPENDICULAR LINES
A) Determining Parallel Lines
1. Parallel lines are lines that will not meet
however far they are produced either way.
2. They are at the same distance apart from
one other
For example :-
(a)
KL is parallel to RS or KL//RS
(b)
AB//CD
(c)
EF//HG
EH//FG
3. To determine wheter two given lines are parallel
or not, follow the steps below.
Step 1
Mark two points P and R on of two straight lines.
The points should be as far apart as possible.
Step 2
Using a protractor ora set aquare draw the two
perpendicular lines PM and RN as shown.
Step 3
Measure PM and RN. The given lines are parallel
to each other if PM =RN.
B) Drawing Parallel Lines
There are three methods to draw parallel lines.
Method 1 : Using a ruler
(a)
(b)
Method 2 : Using a protractor
(a)
(b)
Therefore, PM//RN
Method 3 : Using a set square
(a) To draw a straight line through the point P and
parallel to the straight line XY.
(b)
(c)
(d)
C) Determining Perpendicular Lines
1. If two straight lines intersect at 90 , we say the two
lines are perpendicular to each other.
For example :-
3. We can use a protractor or a set square to determine
wheter two straight lines are perpendicular to each
other or not.
For example :-
(a)
(b)
D) Drawing Perpendicular Lines
1. To draw a line perpendicular ti PR from a point M
on PR, follow the steps as shown below.
Step 1
Step 2
Join MN. The straight line MN will be perpendicular
to PR at M.
2. To draw a line perpendicular to PR from a point M
outside PR, follow the steps below.
Step 1
Step 2
INTERSECTING LINES AND
THEIR PROPERTIES
A) Identifying Intersecting Lines
We say the two straight lines intersect if they meet
( or cut ) at a point. This point is known as the point
of intersection.
For example :-
B) Identifying Complementary Angle
and Supplementary Angles
1. We know that when two lines are perpendicular,
the angle formed by them is a right angle or 90 .
2. Two angles which add up to 90 are called comple-
mentary angles. Each is the complement of the
other.
For example :-
3. We know that the sum of the angles on a atraight line
is 180.
4. Two angles which add up to 180 are called supplemen-
tary angles. Each is the supplement of the other.
For example :-
C) Determining Complementary and
Supplementary Angles
Worked Example 7
Find the value of x in each of the following.
(a) (b)
Solution
D) Identifying Adjacent Angles on a
Straight Line
1. When two straight lines intersect, the sum of the
adjacent angles on a straight line is 180 .
For example :-
The angles x and y which CE makes with the
straight line ACB are called adjacect angles
on a straight line.
Therefore, x + y = 180
2. When two adjacent angles together make
up 180, they are called supplementary angles.
Worked Example 8
Identify the different pairs of adjucent angles
in the following.
(a) (b)
Solution
(a) To determine adjacent angles on a straight
line, measure the angles marked. If the sum
of the angles is 180 , then they are adjacent
angles on a straight line.
x = 60 , y = 120
x + y = 60 + 120
= 180
Therefore, x and y are adjacent angles on the
straight line DEF.
(b) a = 110 , b = 50 , c = 130 , d = 70
a + d = 110 + 70
= 180
Therefore, a and d are adjacent angles on the
straight line PRT.
b + c = 50 + 130
= 180
Therefore, b and c are adjacent angles on the
straight line PRT.
E) Identifying Vertically Opposite Angles
When two straight lines intersect, either pair of
opposite angles are called vertically opposite
angles.
For example :-
Intersection of the straight lines KL and RS.
LINES AND ANGLES
ANGLES A) Identifying an Angle angle is formed by two straigth lines that meet at a point called the vertex. For example : - In the figure above, (a) AOB is an angle. (b) OA and OB are called the arms of the angle. (c) O is the vertex, that is the point where the two arms meet. Worked Example 1 Mark the angle in each case. (a) (b) Solution (a) (b) B) Naming an angle An angle can be named by using one letter or three letters. For example :- Worked Example 2 C) Measuring Angles 1. Angles are measured in units called degrees ( 0 ). 2. To measure an angle, we can use an instru- ment called the protractor as shown below. 3. Note that if we read from left to right ( clockwise direction ), we use the inner scale. 4. To measure an angle less than 1800, <KLM, follow the steps below. Method 1 : Step 1 Place the protactor that its centre is on the vertex L. Adjust the protractor until its base line corresponds with the arm LM. Step 2 Read the value of <KLM using the inner scale. Therefore, <KLM = 300. Method 2 : Step 1 Place the protractor so that its centre is on the vertex L. Adjust the protractor until its base line corresronds with the arm LK. Step 2 Read the value of <KLM using the outer scale. Therefore, .KLM = 300 5. To measure an angle which is more than 1800, follow the steps below : To measure <STU Step 1 Produce the arm ST to V and measure <STV. <STV = 1800 Step 2 Place and adjust the protractor as shown to measure <VTU. Step 3 <STU = <STV + <VTU = 1800 + 200 = 2000 D) Drawing Angles Using a Protractor 1. We can also use a protractor to draw an angle. 2. To draw <RST =600, follow the steps below. Step 1 Draw an arm ST with S as the vertex. Step 2 Place the protractor so that its centre is on the vertex S and its base line is on ST. Step 3 Find 600 at the inner scale and mark it with a point. Call this point R. Step 4 Remove the protractor and draw a line to join R with S. Step 5 Mark and label <RST as 600. 3. To draw <KLM = 2400 ( more than 1800 ), follow the steps below. Step 1 Draw an arm KL with L as the vertex. Step 2 Place the protractor so that its centre is on the vertex L and its base line is on KL. Mark the point M at 600 on the outer scale. Step 3 Remove the protractor and join LM with a straight line. Step 4 Label <KLM as 2400. E) Identifying the Different Types of Angles The table below shows the different types of angles. Worked Example 3 Which of the following angles is acute, obtuse, reflex or right-angled? (a) 1650 (b) 900 (c) 2340 (d) 830 Solution (a) 1650 is an obtuse angle. (b) 900 is right angle. (c) 2340 is a reflex angle. (d) 830 is an acute angle. G) Determining the Sum of Angles on a Straight Line 1. Use a protractor to measure the angles on the straight line. Worked Example 4 Using a protractor, measure the angles on the straingh line KLM. Then, find the sum of the angles in each case. (a) (b) Solution (a) x = 1200 , y = 600 x + y = 1200 + 600 = 1800 (b) p = 400 , q = 900 , r = 500 p + q + r = 400 + 900 + 500 = 180 2. In general, the sum of the angles on a straight line is 1800. For example :- AOB is a straight line. x + y + z = 1800 H) Determining the Sum of Angles in One Whole Turn 1. A protractor is used to measure the angles at a point. Worked Example 5 Use a protractor to measure the angles in the figures. Then, find the sum of the angles in each case. (a) (b) Solution (a) x = 1100 , y = 2500 x + y = 1100 + 2500 = 3600 (b) p = 1300 , q = 600 , r = 700 , s = 1000 p + q + r + s = 1300 + 600 + 700 + 1000 = 3600 2. In general, the sum of the angles that formed one whole turn is 3600. For example :- a + b + c + d + e = 360 I) Calculating Angles involving One Whole Turn Worked Example 6 Without measuring, calculate the angles marked. (a) (b) Solution PARALLEL LINES AND PERPENDICULAR LINES A) Determining Parallel Lines 1. Parallel lines are lines that will not meet however far they are produced either way. 2. They are at the same distance apart from one other For example :- (a) KL is parallel to RS or KL//RS (b) AB//CD (c) EF//HG EH//FG 3. To determine wheter two given lines are parallel or not, follow the steps below. Step 1 Mark two points P and R on of two straight lines. The points should be as far apart as possible. Step 2 Using a protractor ora set aquare draw the two perpendicular lines PM and RN as shown. Step 3 Measure PM and RN. The given lines are parallel to each other if PM =RN. B) Drawing Parallel Lines There are three methods to draw parallel lines. Method 1 : Using a ruler (a) (b) Method 2 : Using a protractor (a) (b) Therefore, PM//RN Method 3 : Using a set square (a) To draw a straight line through the point P and parallel to the straight line XY. (b) (c) (d) C) Determining Perpendicular Lines 1. If two straight lines intersect at 90 , we say the two lines are perpendicular to each other. For example :- 3. We can use a protractor or a set square to determine wheter two straight lines are perpendicular to each other or not. For example :- (a) (b) D) Drawing Perpendicular Lines 1. To draw a line perpendicular ti PR from a point M on PR, follow the steps as shown below. Step 1 Step 2 Join MN. The straight line MN will be perpendicular to PR at M. 2. To draw a line perpendicular to PR from a point M outside PR, follow the steps below. Step 1 Step 2 INTERSECTING LINES AND THEIR PROPERTIES A) Identifying Intersecting Lines We say the two straight lines intersect if they meet ( or cut ) at a point. This point is known as the point of intersection. For example :- B) Identifying Complementary Angle and Supplementary Angles 1. We know that when two lines are perpendicular, the angle formed by them is a right angle or 90 . 2. Two angles which add up to 90 are called comple- mentary angles. Each is the complement of the other. For example :- 3. We know that the sum of the angles on a atraight line is 180. 4. Two angles which add up to 180 are called supplemen- tary angles. Each is the supplement of the other. For example :- C) Determining Complementary and Supplementary Angles Worked Example 7 Find the value of x in each of the following. (a) (b) Solution D) Identifying Adjacent Angles on a Straight Line 1. When two straight lines intersect, the sum of the adjacent angles on a straight line is 180 . For example :- The angles x and y which CE makes with the straight line ACB are called adjacect angles on a straight line. Therefore, x + y = 180 2. When two adjacent angles together make up 180, they are called supplementary angles. Worked Example 8 Identify the different pairs of adjucent angles in the following. (a) (b) Solution (a) To determine adjacent angles on a straight line, measure the angles marked. If the sum of the angles is 180 , then they are adjacent angles on a straight line. x = 60 , y = 120 x + y = 60 + 120 = 180 Therefore, x and y are adjacent angles on the straight line DEF. (b) a = 110 , b = 50 , c = 130 , d = 70 a + d = 110 + 70 = 180 Therefore, a and d are adjacent angles on the straight line PRT. b + c = 50 + 130 = 180 Therefore, b and c are adjacent angles on the straight line PRT. E) Identifying Vertically Opposite Angles When two straight lines intersect, either pair of opposite angles are called vertically opposite angles. For example :- Intersection of the straight lines KL and RS. a and c are vertically opposite angles. b and d are vertically opposite angles. F) Determining the Size of Vertically Opposite Angles If two straight lines intersect, the vertically opposite angles are equal. For example :- G) Finding the Values of Adjacent Angles on a Straight Line Worked Example 9 KLM is a straight line . Find x. Solution H) Problem Solving involving Angles formed by Intersecting Lines Worked Example 10 In the figure above, AB and CD are straight lines. Find the values of x and y. Solution |

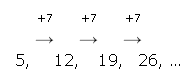














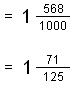



No comments:
Post a Comment